Documentation/4.6/Modules/DiffusionTensorScalarMeasurements
|
For the latest Slicer documentation, visit the read-the-docs. |
Introduction and Acknowledgements
|
| |||||||||||
|
Module Description
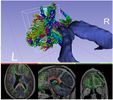
Compute scalar measures from a diffusion tensor dataset. Available measurements include fractional anisotropy, trace, and more.
Use Cases
Most frequently used for these scenarios:
- Use Case 1: Create FA (fractional anisotropy image)
- Use Case 2: Quantify FA or another measure in a region of interest (using also the Editor and Quantification->Label Statistics)
Tutorials
Links to tutorials that use this module
- Slicer4 Diffusion Tensor Imaging Tutorial: https://www.slicer.org/slicerWiki/index.php/Documentation/Nightly/Training#Slicer4_Diffusion_Tensor_Imaging_Tutorial
Panels and their use
Parameters:
- Settings: Input/output parameters
- Input DTI Volume (inputVolume): Input DTI volume
- Output Volume (outputScalar): Scalar volume derived from tensor
- Scalar Measurement (operation): Type of scalar measurement to perform
List of parameters generated transforming this XML file using this XSL file. To update the URL of the XML file, edit this page.
- Trace: trace of the diffusion tensor (equal to the sum of its eigenvalues). Trace = 3 * MD, where MD is mean diffusivity.
- Determinant: determinant of diffusion tensor.
- RelativeAnisotropy: ratio of the anisotropic part of the diffusion tensor to the isotropic part (Basser, 1994)
- FractionalAnisotropy: the degree of anisotropy of diffusion (Between 0 and 1 where 0 = completely isotropic, 1 = completely anisotropic). This measure can be thought of as quantifying how far the shape of diffusion is from a sphere.
- Mode: Quantifies how linear or planar the diffusion is (cigar vs. pancake shape). FA and mode are orthogonal measures. (Ennis & Kindlmann, 2006).
- LinearMeasure: is high in "cigar-shape" tensors, where the first eigenvalue is much larger than the others (Westin, 2002).
- PlanarMeasure: is high in "pancake-shape" planar tensors, where the smallest eigenvalue is much less than the others (Westin, 2002).
- SphericalMeasure: is high where all three eigenvalues are equal, giving a "sphere-shape" of the tensor (Westin, 2002).
- MinEigenvalue: the smallest of the three eigenvalues of the diffusion tensor (also called lambda 3).
- MidEigenvalue: the second smallest eigenvalue of the diffusion tensor (also called lambda 2).
- MaxEigenvalue: the largest of the three eigenvalues of the diffusion tensor (also called lambda 1).
- ParallelDiffusivity: this is equal to the first (maximum) eigenvalue, and also known as lambda 1, axial diffusivity (AD), and longitudinal diffusion coefficient. Note this is equal to MaxEigenvalue, above.
- PerpendicularDiffusivity: this is the average of the smaller two eigenvalues, lambda 2 and lambda 3. This is also known as radial diffusivity (RD) and transverse diffusion coefficient.
Please note that the large number of names for the maximum eigenvalue is due to historical reasons. The original mathematical names are maximum eigenvalue or lambda 1. The names parallel, axial, and longitudinal diffusivity were introduced to help interpret the measure in terms of diffusivity along a hypothesized single fiber tract in the voxel.
Similar Modules
- DWIToDTIEstimation
- FiberTractMeasurements